Método de Burbuja

1. Descripción

El ordenamiento burbuja hace múltiples pasadas a lo largo de una lista. Compara los ítems adyacentes e intercambia los que no están en orden. Cada pasada a lo largo de la lista ubica el siguiente valor más grande en su lugar apropiado. En esencia, cada ítem "burbujea" hasta el lugar al que pertenece. 

La Figura 1 muestra la primera pasada de un ordenamiento burbuja. Los ítems sombreados se comparan para ver si no están en orden. Si hay n ítems en la lista, entonces hay parejas de ítems que deben compararse en la primera pasada. Es importante tener en cuenta que, una vez que el valor más grande de la lista es parte de una pareja, éste avanzará continuamente hasta que la pasada se complete. 

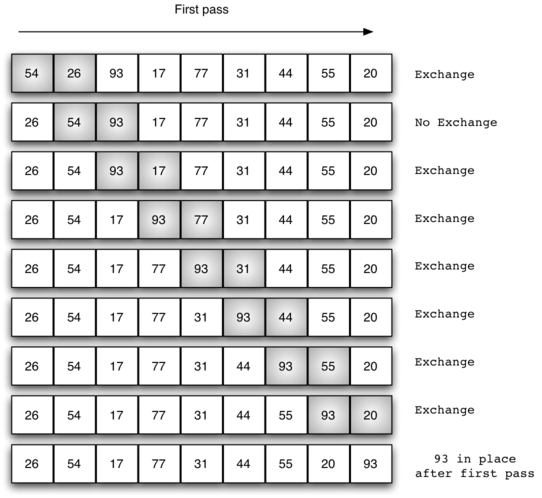
2. Pseudocódigo en C

Tabla de variables

Nombre                     Tipo                                                     Uso
lista                           Cualquiera                                            Lista a ordenar
TAM                          Constante entera                                Tamaño de la lista
i                                 Entero                                                  Contador
j                                 Entero                                                  Contador
temp               El mismo que los elementos de la lista         Para realizar los intercambios

1. for (i=1; i<TAM; i++) 

 2. for j=0 ; j<TAM - 1; j++) 

 3. if (lista[j] > lista[j+1]) 

 4. temp = lista[j]; 

 5. lista[j] = lista[j+1]; 

 6. lista[j+1] = temp;

3. Un ejemplo

Vamos a ver un ejemplo. Esta es nuestra lista:

4 - 3 - 5 - 2 - 1

Tenemos 5 elementos. Es decir, TAM toma el valor 5. Comenzamos comparando el primero con el segundo elemento. 4 es mayor que 3, así que intercambiamos. Ahora tenemos:

3 - 4 - 5 - 2 - 1

Ahora comparamos el segundo con el tercero: 4 es menor que 5, así que no hacemos nada. Continuamos con el tercero y el cuarto: 5 es mayor que 2. Intercambiamos y obtenemos:

3 - 4 - 2 - 5 - 1

Comparamos el cuarto y el quinto: 5 es mayor que 1. Intercambiamos nuevamente:

3 - 4 - 2 - 1 - 5

Repitiendo este proceso vamos obteniendo los siguientes resultados:

3 - 2 - 1 - 4 - 5

2 - 1 - 3 - 4 - 5

1 - 2 - 3 - 4 - 5

4. Optimizando

Se pueden realizar algunos cambios en este algoritmo que pueden mejorar su rendimiento.

• Si observas bien, te darás cuenta que en cada pasada a través de la lista un elemento va quedando en su posición final. Si no te queda claro mira el ejemplo de arriba. En la primera pasada el 5 (elemento mayor) quedó en la última posición, en la segunda el 4 (el segundo mayor elemento) quedó en la penúltima posición. Podemos evitar hacer comparaciones innecesarias si disminuimos el número de éstas en cada pasada. Tan sólo hay que cambiar el ciclo interno de esta manera:

  for (j=0; j<TAM - i; j++)

• Puede ser que los datos queden ordenados antes de completar el ciclo externo. Podemos modificar el algoritmo para que verifique si se han realizado intercambios. Si no se han hecho entonces terminamos con la ejecución, pues eso significa que los datos ya están ordenados. Te dejo como tarea que modifiques el algoritmo para hacer esto :-).
• Otra forma es ir guardando la última posición en que se hizo un intercambio, y en la siguiente pasada sólo comparar hasta antes de esa posición.

5. Análisis del algoritmo

Éste es el análisis para la versión no optimizada del algoritmo:

• Estabilidad: Este algoritmo nunca intercambia registros con claves iguales. Por lo tanto es estable.
• Requerimientos de Memoria: Este algoritmo sólo requiere de una variable adicional para realizar los intercambios.
• Tiempo de Ejecución: El ciclo interno se ejecuta n veces para una lista de n elementos. El ciclo externo también se ejecuta n veces. Es decir, la complejidad es n * n = O(n2). El comportamiento del caso promedio depende del orden de entrada de los datos, pero es sólo un poco mejor que el del peor caso, y sigue siendo O(n2).

Ventajas:

• Fácil implementación.
• No requiere memoria adicional.

Desventajas:

• Muy lento.
• Realiza numerosas comparaciones.
• Realiza numerosos intercambios.

Este algoritmo es uno de los más pobres en rendimiento. Si miras la demostración te darás cuenta de ello. No es recomendable usarlo. Tan sólo está aquí para que lo conozcas, y porque su sencillez lo hace bueno para empezar.

Ejemplo en Lenguaje C:

#include <stdio.h>

void bubbleSort(int arr[], int n) {
int i, j, temp;
for (i = 0; i < n - 1; i++) {
for (j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
// Intercambiar arr[j] y arr[j+1]
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
   }
  }
 }
}

int main() {
int arr[] = {64, 34, 25, 12, 22, 11, 90};
int n = sizeof(arr) / sizeof(arr[0]);
int i;

printf("Arreglo original:\n");
for (i = 0; i < n; i++) {
printf("%d ", arr[i]);
}
printf("\n");

bubbleSort(arr, n);

printf("Arreglo ordenado:\n");
for (i = 0; i < n; i++) {
printf("%d ", arr[i]);
} printf("\n");

return 0;
}

En este código:

• La función bubbleSort toma un arreglo arr y su tamaño n como entrada.
• Los bucles anidados recorren el arreglo, comparando elementos adyacentes.
• Si dos elementos están en el orden incorrecto, se intercambian usando una variable temporal temp.
• La función main declara un arreglo de ejemplo, lo imprime, llama a bubbleSort para ordenarlo y luego imprime el arreglo ordenado.
• El programa primero imprime el arreglo original, luego lo ordena y finalmente imprime el arreglo ordenado.
• El algoritmo de burbuja es fácil de entender e implementar, pero no es muy eficiente para grandes conjuntos de datos debido a su complejidad temporal O(n^2).